题解 华为 OJ

引言

先上图

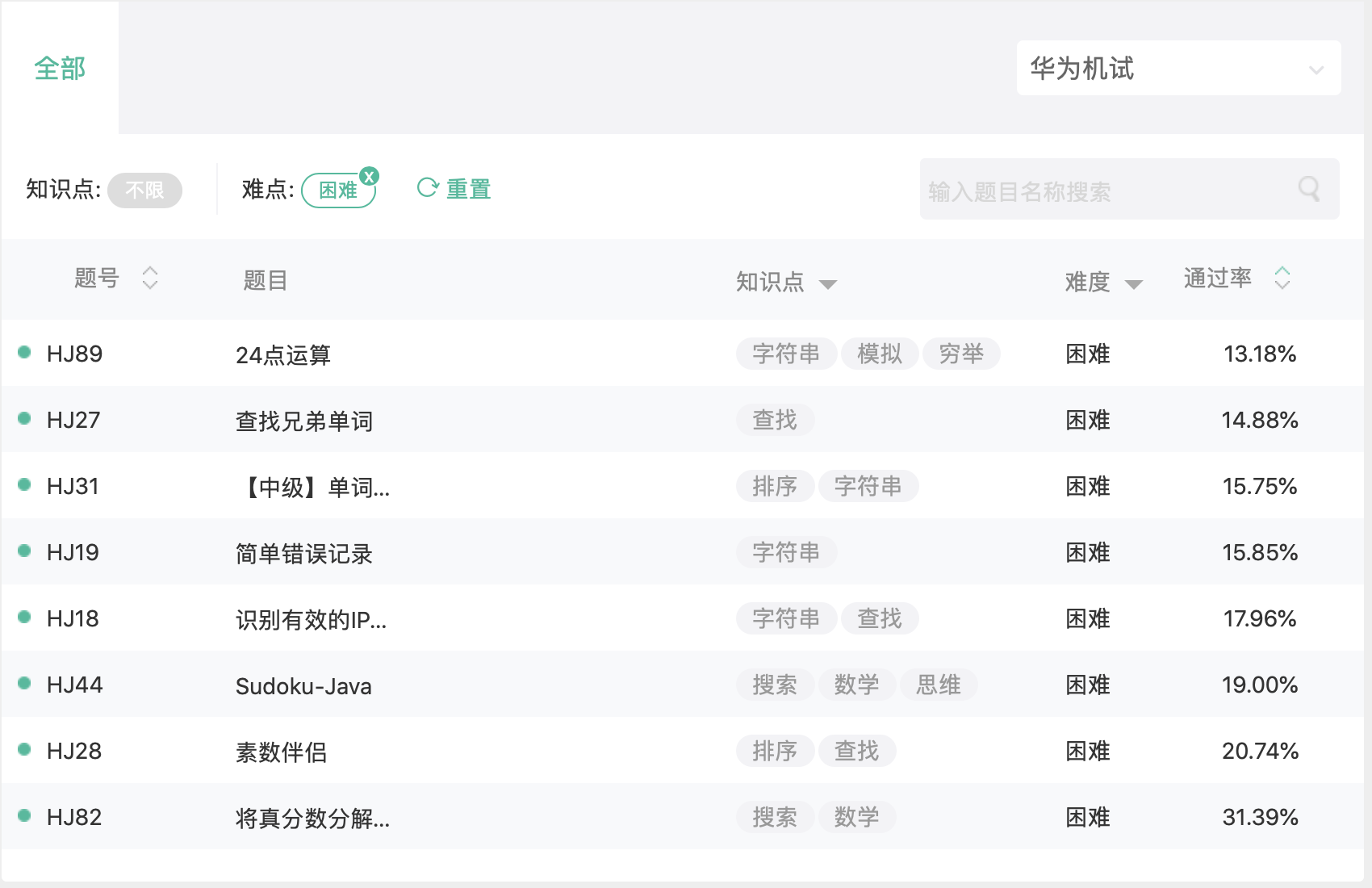
再解释

首先，这是牛客网平台在线编程里华为机试所有困难级别的题，可以看通过率，平均在 20%以下。

不过这个 20%，不是指 5 个人中只有 1 个人解答出来，而是根据所有人提交通过的次数除以总提交次数得到的。不过怎么理解这个比率，并不重要。毕竟，这个“困难”级别就值得商榷。

此外，还有其他几点需要解释的。

1. “查找兄弟单词”这题我没做，原因如下。
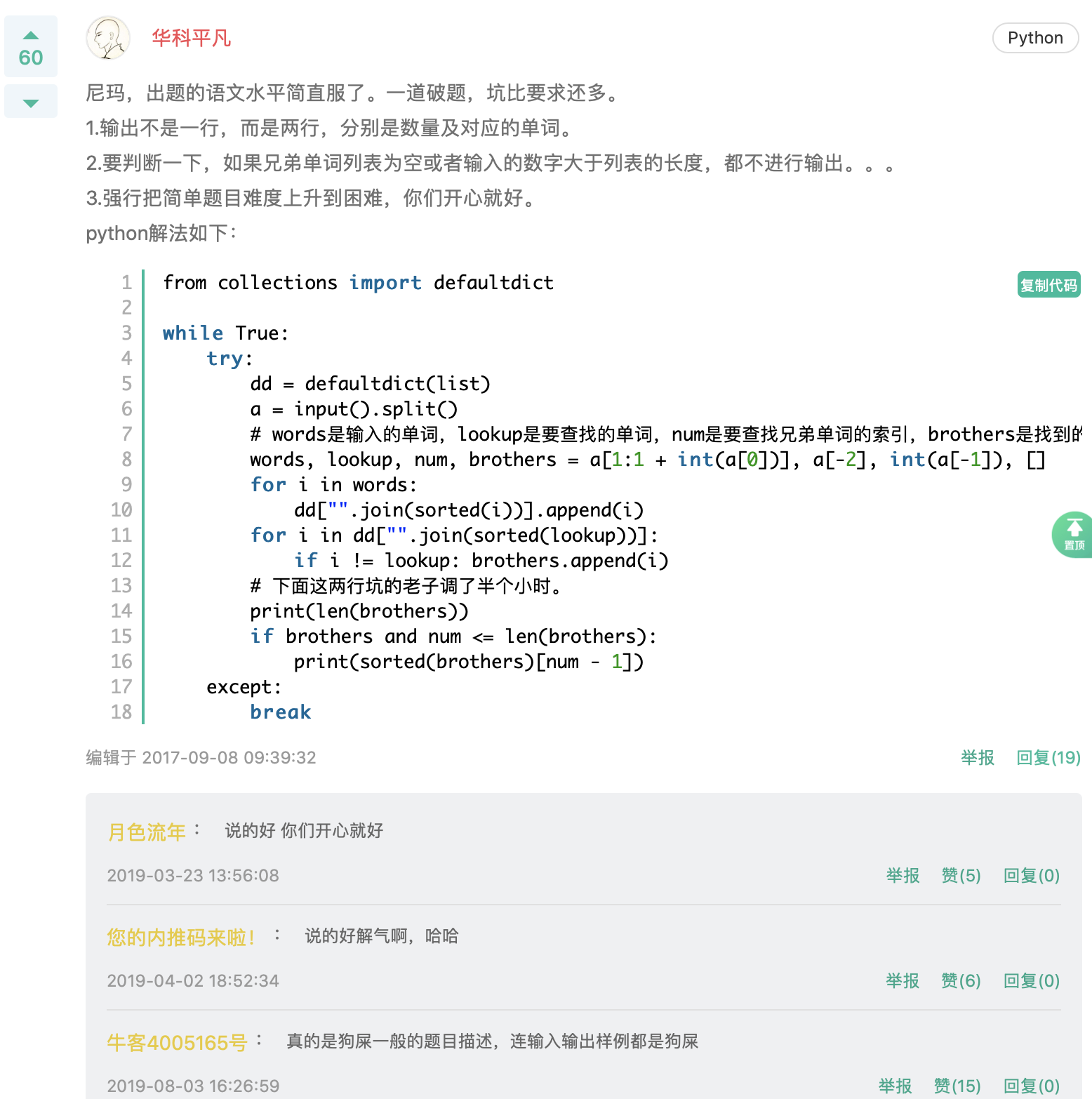
2. ”24 点运算”、“素数伴侣”等部分题，我其实并没有 AC，这一点我要解释一下。

接着 DISS

AC（Accepted，答案正确/通过）本来是程序员挑战一道算法题的最终目标，然而，在**网这里，体验直接为负。

第一大问题：答案不唯一。

例如“真分数分解”这题，给定一个真分数，例如'8/11'，求出其埃及分数的解，即8/11=1/2+1/5+1/55+1/110，但事实上1/2+1/5+1/44+1/220也是对的，当然了第一个解要更优一些，因为最大的分母（110）更小。在标准埃及分数的定义里，确实要有这种优化。这里暂时就不展开了，我在接下来章节会详细讲。这里想说的是，答案不唯一，但后台在验证我们的答案时却是按照后台自己的一套答案去验证的，这就很没意思了。谁有时间跟你这么耗呢？毕竟，你的答案还不一定有我的好，比如以下反馈。

好笑吧~

第二大问题：系统层出不穷的 BUG

第一个问题，也许存在技术上难以解决的问题，大家也都还可以理解。

第二个问题，就 tm 很让人恼火了。

还是以真分数这道题为例，我竟然惊奇地发现最快的 python 答案里，竟然连输出都没有？然后我复制了一遍测试一下，果然能通过。。我真是日了 24k 的钛合金狗眼了。

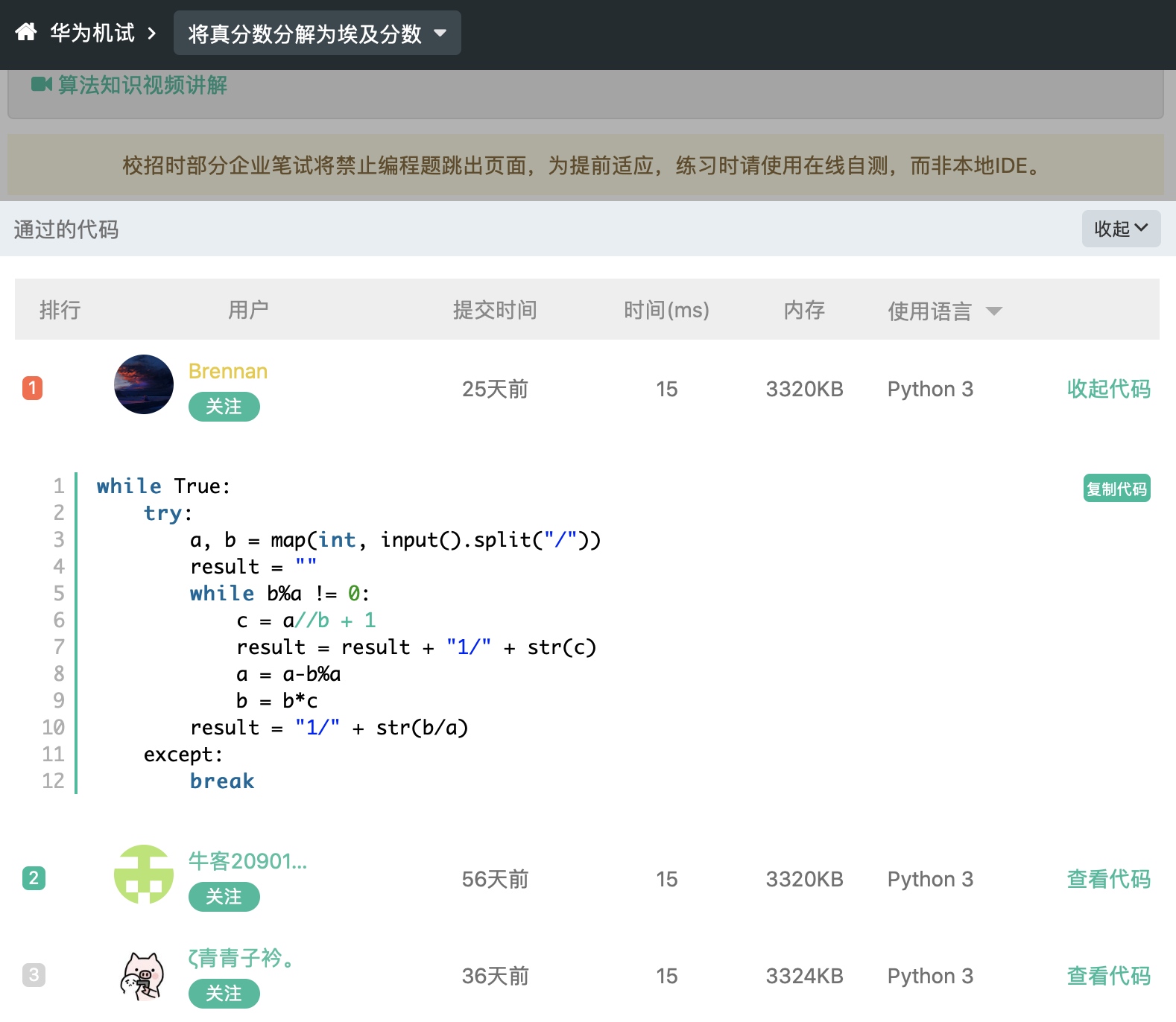
除此之外，我有 30%的概率（甚至更高）在测试模式下，当未通过部分测例时，竟然没有测例显示。我试过清楚 cookie、刷新登录、换浏览器，均无解，失望透顶。

接着，还有 10%的概率，竟然有无法想象的 bug，比如 print 函数竟然还会无效，导致没有输出，我简直笑死。这平台的代码能不能通过，看天。

前端做的已经差不多了，后端是不是缺人啊？多学学友商 Leetcode 吧！

好了吐槽完毕，接下来是正题部分，我将按照我认为的难度、质量水准排序，给出一些解题思考与见解。

华为机试-识别有效的 IP 地址和掩码（分类困难，实际中等）

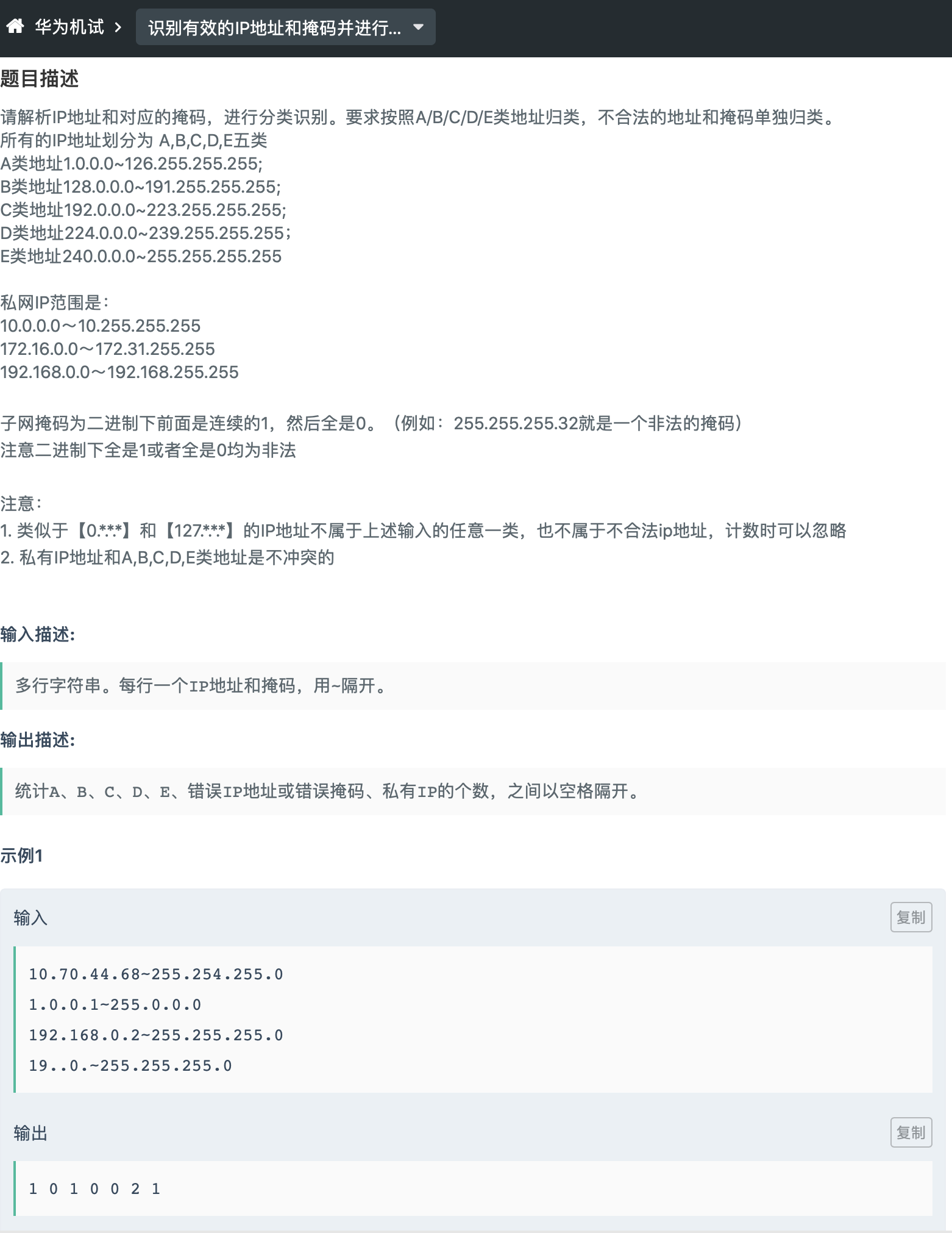
这道题其实挺好的，不但考了一点点算法，还帮助复习了一点点计网。

不过这道题，我觉得对算法唯一有价值的部分是“验证掩码的合法性”。

考虑这句话“子网掩码为二进制下前面是连续的 1，然后全是 0。（例如：255.255.255.32 就是一个非法的掩码） 。注意二进制下全是 1 或者全是 0 均为非法”。

那如果定义一个is_yanma_legal函数，这个函数该怎么写呢？

我从各个题解中，看到一些方法都还是不错的。以下给出各种解法。

掩码判别法一：转二进制后判断 0、1 的相对位置

这是最直观的方法。

不过转二进制有两种方式，如下。

k = 255
assert k.__format__('b') == '11111111'
assert bin(k) == '0b11111111'

对于第二种方法，通过切片选取第三位起即是二进制位。

这里，首先推荐第一种写法，毕竟不需要切片操作。

其次，还得尤其注意占位，我在写的过程中就因为占位问题调试了很长时间。

具体而言，如下：

k = 1
assert k.__format__('b') == '1'
assert k.__format__('08b') == '00000001'

对于第一种写法，在本题掩码判别中将出现问题。

考虑以下掩码：255.1.255.0，按第一种方式得到的二进制掩码为11111111.1.11111111.0左边全是 1 右边全是 0 满足要求；按照第二种方式得到的二进制编码则为11111111.00000001.11111111.00000000，在 1 中有 0 就不满足要求了。

哪种是正确的呢？显然是第二种，所以0 的占位不能丢。

基于此，我们写出第一种判别掩码的方法。（由于在总程序中，我已经先判别掩码是否为标准 IP 地址，因此就不对该函数做字符串验证了。）

def is_yanma_legal(s: str) -> bool:
  s = "".join(map(lambda x: int(x).__format__('08b'), s.split('.')))
  pos_0 = None
  pos_1 = None
  for (p, i) in enumerate(s):
    if i == '1':
      pos_1 = p
    elif i == '0' and pos_0 is None:
      pos_0 = p
  if pos_0 is None or pos_1 is None or pos_1 > pos_0:
    return False
  return True

这段代码，第二句话是核心，就是将十进制的掩码转换为二进制的掩码，接着再确保掩码中有 0、有 1，且最后一个 1 出现的位置在第一个 0 前。

当然了，你也可以用其他方式，比如所有 1 后面紧跟着 1 或者 0，而所有 0 后面都只能为 0，这些都是基于字符串的常规操作。

掩码判别法二：转二进制后通过反码判别（有待改进）

如果一个掩码合法，它的二进制必定全是 1 然后全是 0，基于此，先反码变成全是 0 再全是 1，然后再进行加 1 操作，这时必然变成全是 0 然后 1 个 1 然后全是 0。当然了，左边的 0 不是必须的，这个新的二进制数的关键是只有 1 个 1。

不过，在 python 里面，数字是按照补码进行表示的，这导致0b110这样的二进制数的反码不是0b001，而是它补码的反码的原码表示。

具体而言~0b110 = ~0b00000110，对正数 6 取反，即先对 6 的补码取反考虑符号位再减一，正数 6 的补码为其自身，即0b00000110，该补码的反码为0b11111001，减一后为0b11111000，符号位为 1 即负号，取反为0b00000111，即 7，所以最终结果为-7。

显然，这样的反码操作不是我们相要的，我们仅仅是想让字符串取反而已。

由于我对 python 的位运算也不是很熟悉，所以这里就朴素地实现一下。（还是很繁琐的，对每一位与 1 进行异或运算）。

最后再转换为二进制数加一判断 1 的数目。

def is_yanma_legal(s: str) -> bool:
  s = "".join(map(lambda x: int(x).__format__('08b'), s.split('.')))
  s2 = ''.join(map(lambda x: str(int(x) ^ 1), s))
  s3 = bin(eval('0b' + s2) + 1)[2:]
  # print({'s': s, 's2': s2, 's3': s3})
  return sum(map(int, s3)) == 1

尽管如此，该程序仍会有 bug，那就是对0.0.0.0与255.255.255.255的识别，会变成True，这主要是由于进位之类的原因导致的。所以对位运算不熟悉不要考虑该种方案。

掩码判别法三：位运算过渡态

其实我认为，第三种方案，是最有含金量的。

考虑一个十进制的掩码255.254.0.0，它是合法的吗？我们写一下它的二进制掩码：11111111.11111110.00000000.00000000，可以看到，是符合要求的。

注意第二个数，254。这个数有什么特点呢？显然，这个数，其二进制自身就满足左边全是 1 右边全是 0。

那么整个掩码的四个数字构成就有三种：二进制全是 1，即 255；二进制全是 0，即 0；二进制左边是 1，右边是 0，这样的数一共有 6 个，即11111110, 11111100, 11111000, 11110000, 11100000, 11000000, 10000000，这 6 个数，其实分别就是

255-2^0 = 254
255-2^0-2^1 = 252
255-2^0-2^1-2^2 = 248
255-2^0-2^1-2^2-2^3 = 240
255-2^0-2^1-2^2-2^3-2^4 = 224
255-2^0-2^1-2^2-2^3-2^4-2^5 = 192
255-2^0-2^1-2^2-2^3-2^4-2^5-2^6 = 128

事实上，对于这样的数，直接用位运算就更直观了：

255 & 255 << 1 = 254
255 & 255 << 2 = 252
255 & 255 << 3 = 248
255 & 255 << 4 = 240
255 & 255 << 5 = 224
255 & 255 << 6 = 192
255 & 255 << 7 = 128

由此，可以写出更加优美的判断掩码函数。

OPTS = [255 & 255 << i for i in range(0, 9)]

def is_yanma_legal(s: str) -> bool:
  last_num = None
  for num in s.split('.'):
    num = int(num)
    # 掩码内每个数字，只能有9种
    if num not in OPTS:
      return False
    # 掩码不能全是0
    if last_num is None and num == 0:
      return False
    # 掩码的中间只能有一个左1右0的数
    if last_num and last_num < 255 and num != 0:
      return False
    last_num = num
  # 掩码不能全是255
  return num != 255

可以执行以下判断测试：

assert(is_yanma_legal('255.255.255.255') == False)
assert(is_yanma_legal('0.0.0.0') == False)
assert(is_yanma_legal('255.0.0.0') == True)
assert(is_yanma_legal('255.255.128.0') == True)
assert(is_yanma_legal('255.83.255.255') == False)

华为机试-简单错误记录（标注困难，实际简单）

这题，没啥好说的，就讲两点吧。

第一点，路径分隔符

一般来说，在 windows 平台，路径是以\\双反斜杠分隔的；在 linux 平台与 mac 平台是以/单斜杠分隔的。

而题目的测例竟然是\单反斜杠分隔的，也是极其迷了。

这有什么不良影响呢？那就是os.path.basename这样的基于操作系统路径得到文件名的函数就没用了。

第二点，获取文件名

至少有四种方法。

首先以测例为例：E:\V1R2\product\fpgadrive.c。记该路径为K。

第一种，直接用split函数。

K.split('\\')[-1].split('.')[0]

第二种，使用正则。

import re
re.search(r'\(\w+)\.\w+$').groups()[0]

第三种，使用os库。

本题不适用，不过，假设`K='E:\V\product\fpgadrive.c'，即标准 windows 路径。

import os
os.path.splitext(os.path.basename(K))[0]

值得注意的是，直接使用str.split('.')[0]得到的是第一个点之前的字符串，而os.path.splitext(file_name)[0]得到的则是最后一个点之前的字符串，这在文件名里有多个后缀时将会有差异，比如my_photo.png.backup。

第四种，使用pathlib库。

from pathlib import Path
Path(K).stem

最为简单，直接得到不带后缀的文件名，不过也要求K是个标准路径。如果需要获得带后缀的文件名，则使用Path(K).name。

不过其实，pathlib库看起来好用，在实际项目中还是会遇到一些比较麻烦的问题，比如原作基于os.path得到的是一些文件路径的字符串，而使用pathlib转换文件路径之后，则必须得使用Path.resolve()等函数获得字符串类型的路径。

华为机试-单词倒排（标注困难，实际简单）

这道题用 python 处理起来十分简单，并且评论区出现了一些一行代码的解决方案。

然而，我必须指出，这些代码是有问题的。

例如：

print(" ".join(input().replace("*"," ").replace("#"," ").replace("!"," ").replace("$"," ").split()[::-1]))

这行代码里对输入中的* # ! $这四个符号进行了空白替换，这显然是根据用例来的，这样的解决方案我们不能要。

正确的一行解决方案如下。

print(" ".join("".join([i if i.isalpha() else " " for i in input()]).replace('  ', '').split()[::-1]))

代码虽然可读性变差了， 但其实更短，而且也不难理解。就是把字符分为字母类与非字母类。非字母类统一换成空格，然后再将字符串起来并替换掉所有连续空格为单独的空格，再根据单独的空格进行列表切割，最后再倒序拼接。

华为机试-查找兄弟单词（标注困难，实际简单，题目模糊，建议跳过）

没啥好说的，直接跳过。

华为机试-数独（标注困难，实际较难）

这题就是一个标准的数独问题。

很显然，这题是可以有一些效率较高的动态规划方法的，因为每填一个数字，对后续的都会有影响。

我的解决方案：DFS 回溯

先给一下我的解决方案，主要思想就是基于深度搜索的回溯。

首先通过get_opts函数，用以判断每一个待定的单元格；其次使用back_fill函数进行填充。对于待定单元格，如果发现待定可能数为 1，则直接填充；如果待定可能为 0，说明进入了死胡同，则回溯（时光穿梭回上一个历史记录）；如果待定可能大于 1，则为每一种可能创建一个时光快照。

由于数独的大小为 9*9，不大，而且需要填充的单元格不可能很多，因此回溯法完全可以 AC。

SET = {1, 2, 3, 4, 5, 6, 7, 8, 9}


def get_opts(x, y, arr):
    bans = set()
    # 列
    for row_no in range(9):
        if arr[row_no][y] != 0:
            bans.add(arr[row_no][y])
    # 排
    for col_no in range(9):
        if arr[x][col_no] != 0:
            bans.add(arr[x][col_no])
    # 小宫格
    for row_no in range(x - x % 3, x + 3 - x % 3):
        for col_no in range(y - y % 3, y + 3 - y % 3):
            if arr[row_no][col_no] != 0:
                bans.add(arr[row_no][col_no])
    return SET - bans


def back_fill(arr, history=[]):
    for x in range(9):
        for y in range(9):
            if arr[x][y] == 0:
                opts = get_opts(x, y, arr)
                if len(opts) == 1:
                    arr[x][y] = opts.pop()
                elif len(opts) == 0:
                    return back_fill(history[-1], history[:-1])
                else:
                    for opt in opts:
                        arr2 = [row[:] for row in arr]
                        arr2[x][y] = opt
                        history.append(arr2)
                    return back_fill(history[-1], history)
    return arr


def export(s):
    arr_input = [[int(i) for i in line.split()] for line in s]
    # print({'arr_input': arr_input})

    arr_output = back_fill(arr_input)
    # print({"arr_output": arr_output})
    for line in arr_output:
        print(' '.join([str(i) for i in line]))

python 最快解决方案：无记忆式回溯

其实我们给的两种解决方案，模型都是一样的，不过写法和设计上还是有一定区别。

我之所以粘贴他的这份方案，是因为我觉得，他写的确实很有意思。

他定义了一个函数f(num)，num从 0 到 81，代表单元格确定的个数。显然当num大于 80 时，整个数独就填充完成了。

此外，他也没有对每一个矩阵进行快照存储，而是直接使用a[row][col]=0和a[row][col]=i等标记方式实现回溯的更新。

我和他的解题速度相差一倍左右。

a = []
def check(row, col, v):
    for k in range(9):
        if a[row][k] == v or a[k][col] == v: return False
    t = row//3
    q = col//3
    for k in range(t*3,t*3+3):
        for p in range(q*3,q*3+3):
            if a[k][p] == v: return False
    return True
def f(num):
    global a
    if num > 80: return True
    row = num // 9
    col = num % 9
    if a[row][col] != 0: return f(num+1)
    else:
        for i in range(1,10):
            if check(row,col,i):
                a[row][col] = i
                if f(num+1): return True
                else: a[row][col] = 0
        return False

while True:
    try:
        for i in range(9):
            b = list(map(int,input().split()))
            a.append(b)
        f(0)
        for i in range(9):
            print(' '.join(map(str,a[i])))
    except:
        break

华为机试-24 点运算（标注困难，实际较难）

题目

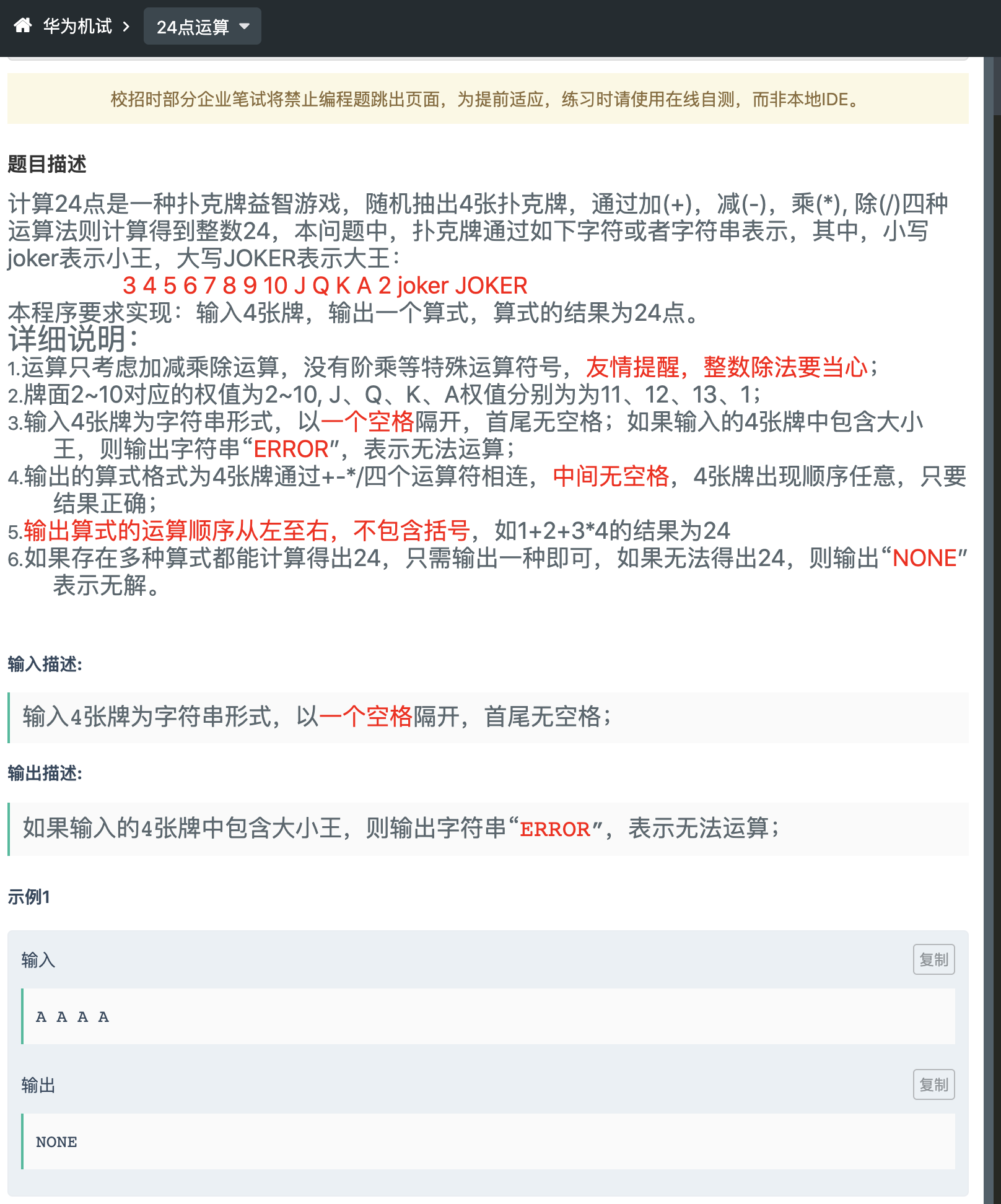
思路

这题就更有意思了，毕竟我对 24 点十分有感情，小学数学竞赛一开始接触的就是这个，算是数学上的启蒙游戏了。

不过这道题有一点遗憾，因为它不支持括号运算，尽管可以任意调换数字位置，但是不支持括号运算直接导致一些高级操作无法实现，比如经典 24 点题：输入：3 3 7 7； 输出： 7 * ( 3 + 3 / 7 ) = 24。没有括号的话，是无法得到答案的。

对于这道题，我先后想了一些有趣的方案，其中一种还借鉴了会计学里的会计平衡式，hhh。（然并卵）

最后我把之前想的方案都否了，因为看了这个点赞最高的题解。

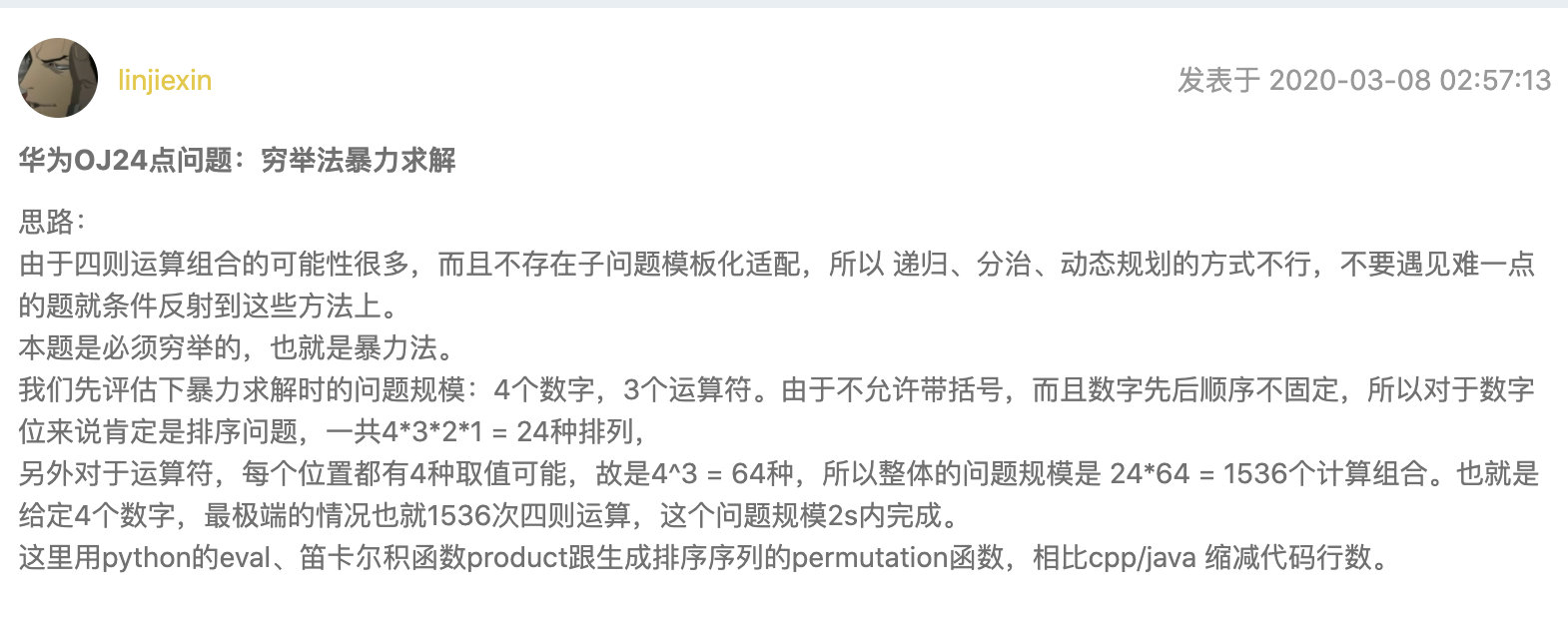
没错啊，算个 24 点，穷举一下也就 1000 多个有限运算而已。。。实在没啥好怕的啊！

不过这里有一个有意思的库需要提一下：itertools。

itertools 库

itertools 库里提供了一些很有用的迭代、组合有关的函数。

首先就是笛卡尔积itertools.product，直接看用例就可以理解了。

>>> [i for i in itertools.product([1, 2, 3], repeat=2)]
[(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3)]

所以在这道题里，每张牌的位置特别适合使用笛卡尔积进行迭代。

其次就是全排列itertools.permution，也直接看用例就可以理解了。

>>> [i for i in itertools.permutations([1, 2, 3])]
[(1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1)]

所以在这道题里，运算符号的位置就特别适合使用全排列进行迭代。

两个函数的具体应用，可以见下面我的解决方案。

我的解决方案

最后我给出的最终方案如下：

import itertools

CHAR_DICT = {'J': 11, 'Q': 12, 'K': 13, 'A': 1}
OPER_LIST = ['+', '-', '*', '/']

def solve(s):
    arr = []
    for i in s.strip().split(" "):
        if i in ['joker', 'JOKER']:
            return 'ERROR'
        arr.append(CHAR_DICT[i] if i in CHAR_DICT else int(i))

    for a in itertools.permutations(arr):
        for i, j, k in itertools.product(OPER_LIST, repeat=3):
            expression = '{}{}{}{}{}{}{}'.format(a[0], i, a[1], j, a[2], k, a[3])
            if eval(expression) == 24:
                return expression
    return 'NONE'

if __name__ == '__main__':
    while True:
        try:
            print(solve(input().strip()))
        except EOFError:
            break

代码还是美的，只不过并没有 AC。

（很好，截图截到一个 BUG，练习模式用例未全部通过，竟然不显示错误的用例，辣鸡，其他题是显示的，其他人也是显示的， 就我。。）

不过，这个没有 AC，我并不在意，因为每种牌的运算方案不一定是唯一的。

python 最快方案（很朴素）

最后，再给一份 AC 了的最快速度的代码，这代码写的通俗又有趣，hh。

dict1 = {'A': 1, 'J': 11, 'Q': 12, 'K': 13}
opt = ['+', '-', '*', '/']
while 1:
    try:
        li = input().split()
        if 'joker' in li or 'JOKER' in li:
            print('ERROR')
            break
        list1 = []
        for i in li:
            if i in dict1.keys():
                list1.append(dict1[i])
            else:
                list1.append(int(i))
        rs = False
        for i in range(4):
            for j in range(4):
                if j != i:
                    for k in range(4):
                        if k not in [i, j]:
                            index = [0, 1, 2, 3]
                            index.remove(i)
                            index.remove(j)
                            index.remove(k)
                            m = index[0]
                            num1, num2, num3, num4 = list1[i], list1[j], list1[k], list1[m]
                            for op1 in opt:
                                if op1 == "+":
                                    a1 = num1 + num2
                                if op1 == "-":
                                    a1 = num1 - num2
                                if op1 == "*":
                                    a1 = num1 * num2
                                if op1 == "/":
                                    a1 = num1 / num2
                                for op2 in opt:
                                    if op2 == "+":
                                        a2 = a1 + num3
                                    if op2 == "-":
                                        a2 = a1 - num3
                                    if op2 == "*":
                                        a2 = a1 * num3
                                    if op2 == "/":
                                        a2 = a1 / num3
                                    for op3 in opt:
                                        if op3 == "+":
                                            a3 = a2 + num4
                                        if op3 == "-":
                                            a3 = a2 - num4
                                        if op3 == "*":
                                            a3 = a2 * num4
                                        if op3 == "/":
                                            a3 = a2 / num4
                                        if a3 == 24:
                                            rs = True
                                            print("%s%s%s%s%s%s%s" % (li[i], op1, li[j], op2, li[k], op3, li[m]))
                                            break

        if not rs:
            print("NONE")
    except:
        break

篇幅过长了，以下两篇重磅题型，留待下篇更，都有我独特的见解！

华为机试-将真分数分解为埃及分数

题目描述

分子为 1 的分数称为埃及分数。现输入一个真分数(分子比分母小的分数，叫做真分数)，请将该分数分解为埃及分数。如：8/11 = 1/2+1/5+1/55+1/110。

（南川补充：此外，每个埃及分数的分母不得重复）

输入描述

输入一个真分数，String型

输出描述

输出分解后的string

示例一

输入

8/11

输出

1/2+1/5+1/55+1/110

思路一：迭代+深搜索

这道题如果第一次见，还是比较难的，原因在于我们并不知道一个真分数最终将由几个埃及分数构成。如果直接使用暴力枚举，我们也很难理清枚举的上限。

但这道题有个关键的约束，就是目标分数小于 1，而每个埃及分数的分子都是 1，这就使每一个埃及分数的可能值有了一定的确切边界。

考虑示例中的8/11，假设我们首先尝试第一个最大的埃及分数为1/2，这就导致其余的埃及分数必然小于8/11-1/2=15/22；

接着再尝试第二个最大的埃及分数1/3，使得剩余分数必然小于15/22-1/3=23/66；

接着是1/4，剩余分数为23/66-1/4=8/132。而这个数，已经有点不一样了。因为接下来如果再加一个埃及分数的话，那么它必须小于1/17，也就是中间的5-16都不用试了。

很显然，如果我们紧接着再加上一个1/17 ，接下来的数将更小。以此往复。

因此，我们必须要定义剪枝条件，否则这将迭代没有尽头。

剪枝的目标

为了更好地剪枝，我们需要再次明确问题的优化目标。

根据埃及分数的问题背景，我们补充对题的理解。

首先，显然埃及分数的解不唯一。举个例子：4/24=1/6=1/8+1/24，这已经是两种埃及分数分解的方案。

因此我们迭代过程中有必要思考一下其他的优化目标。

其中第一个额外目标就是，使埃及分数的个数最小，如上，1/6就要明显优于1/8+1/24。

第二个额外目标就是，在同个数的情况下，最小的埃及分数尽可能大，也就是说最大的分母尽可能小，这些都是非常符合常识的。

剪枝的关键

其实，两个额外目标（个数少，分母小）之间还有微妙的制衡关系。

例如，我们假设期望最大个数为 3，考虑 8/11 这个真分数，在尝试使用1/2+1/3这两个埃及分数之后，显然，仅仅考虑第一个额外目标我们就知道，此路不通，因为没有任何一个埃及分数等于23/66，因此不可能仅仅通过三个埃及分数（其中两个为1/2和1/3）。

于是，迭代开始回溯，我们继续考虑考虑1/2+1/4。容易知道，依旧没有合适的解。

紧接着，我们发现，，只要第一个埃及分数是1/2，总埃及分数限制不超过 3，接下来几乎都没有解，但我们总不能一直迭代下去吧？实际上这里也有隐含剪枝条件，也就是从 2 倍的埃及分数必须大于等于剩余分数，否则继续遍历将始终小于剩余分数，没有意义。

基于此，我们发现，只要设定了第一个目标（埃及分数个数不超过 K），第二个目标就几乎无需考虑，因为对于第 i 个埃及分数，始终有一个剪枝条件就是f(i)*(K-i)>=F(i)，这里的f(i)指第 i 个埃及分数的值，F(i)指剩余分数大小。在遍历的过程中一旦不满足，即可回溯，直到当i=1时也不满足才返回没有结果的异常。例如对于目标分数8/11，目标最大个数为3的情况，当对第一个埃及分数遍历超过 4 时，即可直接返回异常，因为1/5 * 3 < 8/11。

由此，我们可以写出一个能在有限时间内找到解的算法，唯一的问题就是必须限制埃及分数的最大个数。

思路一的编程实现：DFS

考虑到这题只是一个机试，因此，测例还是比较友好的，我们姑且设置埃及分数的最大个数为 5。

这里，值得注意的是，分数加减有精度误差，判等时需要做精度控制。

编写如下代码。

import math
PRECISION = 1e-16
MAX_DENOMINATOR = 1000

def DFS(target):
    def solve(target, chain, n):
        L = max(math.floor(1 / target), 1 + chain[-1] if chain else 0)
        R = min(math.ceil((n - len(chain)) / target) + 1, MAX_DENOMINATOR)
        # print({'target': round(target, 4), 'chain': chain, 'L': L, 'R': R})
        for i in range(L, R):
          # 控制差小于精度，等价于数相等
            if abs(1/i - target) < PRECISION:
                ans_list.append('+'.join(['1/' + str(i) for i in chain + [i]]))
            elif len(chain) < n and target > 1/i:
                ans = solve(target - 1 / i, chain + [i], n)
                if ans:
                    return ans

    ans_list = []
    solve(target, [], 4)
    print('Possible ans: ')
    for ans in ans_list:
        print(ans)

对于DFS(8/11)的结果如下，它列出了最多四个埃及分数的可能的解。

Possible ans:
1/2+1/5+1/40+1/440
1/2+1/5+1/44+1/220
1/2+1/5+1/45+1/198
1/2+1/5+1/55+1/110
1/2+1/5+1/70+1/77
1/2+1/6+1/17+1/561
1/2+1/6+1/18+1/198
1/2+1/6+1/21+1/77
1/2+1/6+1/22+1/66
1/2+1/7+1/12+1/924
1/2+1/7+1/14+1/77
1/2+1/8+1/10+1/440
1/2+1/8+1/11+1/88
1/3+1/4+1/7+1/924

思路一的优化：BFS

虽然上述 DFS 的方法，已经能够解决这道题，但它只是简单罗列了所有满足最大固定子分数个数的解而已，假设一个真分数既可以展开成 3 个埃及分数，也能展开 4 个，使用 DFS 将必须迭代获得所有解最后才能知道最优解，显然有效率优化的空间。而解决方案就是 BFS。

使用 BFS，我们可以针对性地按行遍历，先遍历只使用 1 个埃及分数的情况，若无解再扩展成 2 个，接着是 3 个，直到有解。而要实现 BFS 的关键就是使用队列，因此我们简单修改一下原来的代码，使之满足 BFS 的要求。

此外，由于使用 BFS 横向搜索，所以有必要定义一个分母上限，防止搜索过长。这想起来其实挺有意思的，虽然无论使用 DFS 还是 BFS，搭配使用最大分母上限与最大个数上限都有助于提高算法效率。但相对来说，DFS 更依赖最大个数上限（也就是层数限制），而 BFS 更依赖最大分母上限（即每层的个数上限）。

代码如下。

from queue import Queue
import math
PRECISION = 1e-16
MAX_WIDTH = 5
MAX_DENOMINATOR = 1000


def is_equal(target, i):
    return abs(target - 1/i) < PRECISION


def run(target):
    q = Queue()
    ans_list = []

    def layer_solve(target, chain):
        L = max(math.ceil(1/target), chain[-1]+1 if chain else 2)
        for i in range(L, MAX_DENOMINATOR):
            if is_equal(target, i):
                ans_list.append(chain + [i])
                return
            # 判断是否找到解，一旦找到，便不再纵向遍历
            elif 1/i < target and len(ans_list) == 0:
                if (MAX_WIDTH - len(chain)) / i >= target:
                    q.put((target-1/i, chain+[i]))
                else:
                    break

    layer_solve(target, [])
    while not q.empty():
        layer_solve(*q.get())

在这段代码中相较于上段代码，首先是引入了queue包，此外单独抽离出判等函数，使算法的逻辑更清晰，可扩展性更强。

简单运行测例run(8/11)可以得到如下结果。

ans_list:
[2, 5, 40, 440]
[2, 5, 44, 220]
[2, 5, 45, 198]
[2, 5, 55, 110]
[2, 5, 70, 77]
[2, 6, 17, 561]
[2, 6, 18, 198]
[2, 6, 21, 77]
[2, 6, 22, 66]
[2, 7, 12, 924]
[2, 7, 14, 77]
[2, 8, 10, 440]
[2, 8, 11, 88]
[3, 4, 7, 924]

看上去和 DFS 的结果没啥区别，也是 4 层。

但是，如果我们换一个测例，比如run(3/13)，差异就体现出来了。

ans_list:
[5, 35, 455]
[5, 39, 195]
[5, 45, 117]
[6, 16, 624]
[6, 18, 117]
[6, 26, 39]
[7, 13, 91]

可以看到，所有的解都只有三个元素，说明算法在第三层即找到解，而避免了搜索第四层，这显然是满足了我们优化算法的目标的。

Python 对分数处理的另一种替代方案

Python 其实有一个内置包叫fraction用于处理分数，两个Fraction对象相减得到的结果也是Fraction，此外还会自动月分，比如Fraction(2, 4)这个数，它就等于Fraction(1, 2)，如果调用它的numerator（分子）属性会发现就等于 1，相应地，它的denominator（分母）属性就是等于 2。这样的性质非常适合用来解决这道题，因为它首先避免了精度损失，此外还可以在判等时直接判断分子是否为 1，效率应该是更高的（至少可读性更高）。

以下简单给出一份基于Fraction的代码。

from fractions import Fraction
import math

PRECISION = 1e-16
MAX_DENOMINATOR = 1000


def DFS_fraction(target):

    def solve(target: Fraction, chain, n):
        if target.numerator == 1:
            ans_list.append('+'.join(['1/' + str(i) for i in chain]))
        elif len(chain) < n:
            L = max(math.ceil(1 / target), 1 + chain[-1] if chain else 0)
            R = min(math.ceil((n - len(chain)) / target) + 1, MAX_DENOMINATOR)
            # print({'target': target, 'chain': chain, 'L': L, 'R': R})
            for i in range(L, R):
                solve(target - Fraction(1, i), chain + [i], n)

    ans_list = []
    solve(Fraction(target), [], 3)
    print('ALL THE ANS: ')
    for ans in ans_list:
        print(ans)


if __name__ == '__main__':
    DFS_fraction(4 / 13)

不过值得注意的是，尽管基于Fraction的处理是精确的，但是仍然会有一些违反普通人常识的设计，比如当多个分数相减，导致值为 0 时，可能会出现以下的结果。例如：

我们其实早已经知道8/11 = 1/2 + 1/5 + 1/55 + 1/110，然而通过分数计算得到的结果却让我们有一些难以接受，尽管如此，在处理分数加减上，它还是比纯粹使用浮点数，来的更人性化一些。

如果你的项目需要频繁处理财务之类的数据，那么强烈推荐你了解fraction这个模块，比如在四大工作的朋友们。

思路二：数论解法

首先上链接：埃及分数(迭代加深搜索，斐波那契分解分数)_zyz_bz 的博客-CSDN 博客

接着上公式。

$$when a<b, a\in N^+,b\in N^+, \\ let b=a*p+r, p=a//b, r=a\%b, then \\ \frac{a}{b} = \frac{a}{a*p+r} = \frac{(ap+r)+(r-a)}{(a*p+r)(p+1)} = \frac{1}{p+1}+\frac{a-r}{(a*p+r)(p+1)}$$

这就是大名鼎鼎的斐波那契分解法，我们很容易得知$\frac{a}{b}$可以分解为$\frac{1}{p+1}$（一个埃及分数）与另外一个分数。

这里，最值得注意的是，第二个分数的分子比原分数要小（$r>0, a-r<a$），因此对第二个分数继续展开，总能在有限次数下压缩到最小（即分子为 1）。

此外，若我们记$r=0$，可以立即得到该分数变成$\frac{1}{p*(p+1)}$，它正是一个埃及分数。

总之，我们容易得证，该分解是收敛必有解的。

基于此，我们实现更帅气的数论解法。

思路二的编程实现：基于数论

直接使用递归实现。

def run(a: int, b: int):

    def solve(a: int, b: int):
        print({'a': a, 'b': b})
        p = b // a
        r = b % a
        yield p+1

        a_ = a - r
        b_ = (a*p+r) * (p+1)

        if a_ == 1:
            yield b_
        else:
            yield from solve(a_, b_)

    ans = ' + '.join('1/%d' % i for i in solve(a, b))
    print('ANS of {} / {}'.format(a, b))
    print(ans)
    return ans


if __name__ == '__main__':
    run(8, 11)

结果如下：

{'a': 8, 'b': 11}
{'a': 5, 'b': 22}
{'a': 3, 'b': 110}
ANS of 8 / 11
1/2 + 1/5 + 1/37 + 1/4070

可以看到，只要执行几次函数就得到结果，不得不说，速度是搜索法的上百倍甚至上万倍。。。

唯一的缺点就是受限于该数论的分解范式，很难得到最优的解，除非我们对我们的斐波那契分解做更细致地调整。

基于此，我是不满意目前的结果的，但我也无法从数论角度给出更好的解决方案了，毕竟，这个分解关系式，我是想不出来的。

此处假装 at 数论大神。

该题总结

这题真地还是很有意思的，只要你想深挖，可以充分锻炼自己的 DFS、BFS 算法设计能力，包括搜索时的技巧（而非简单的搜索）。

最后，借着数论的解决方法再度升华本题的价值，实属经典，我也就不吝啬笔墨了。

华为机试-素数伴侣

题目描述

若两个正整数的和为素数，则这两个正整数称之为“素数伴侣”，如 2 和 5、6 和 13，它们能应用于通信加密。现在密码学会请你设计一个程序，从已有的 N（N 为偶数）个正整数中挑选出若干对组成“素数伴侣”，挑选方案多种多样，例如有 4 个正整数：2，5，6，13，如果将 5 和 6 分为一组中只能得到一组“素数伴侣”，而将 2 和 5、6 和 13 编组将得到两组“素数伴侣”，能组成“素数伴侣”最多的方案称为“最佳方案”，当然密码学会希望你寻找出“最佳方案”。

输入描述

输入说明
1 输入一个正偶数n
2 输入n个整数

输出描述

求得的“最佳方案”组成“素数伴侣”的对数。

示例 1

输入

4
2 5 6 13

输出

2

解题思路

本题需要使用匈牙利算法，对该算法不了解的先移步我另外一篇有趣的文章 求解：《三十而已》中王曼妮的恋爱匹配问题？

因为偶数与偶数相加、奇数与奇数相加都必定不是素数。所以可以把偶数和奇数分列两个阵营，也就是二分图，然后使用匈牙利算法求解即可。值得注意的是，对于每一个偶数，对方阵营中是否能与该偶数匹配需要遍历相加判断得出。

代码与测例如下，答案是 25。

def is_prime(x: int):
    for i in range(2, int(x**.5)):
        if x % i == 0:
            return 0
    return 1


def main(s):
    boys = []
    girls = []
    for i in s.split():
        i = int(i)
        if i % 2 == 0:
            boys.append(i)
        else:
            girls.append(i)

    def find_girl(boy_i):
        for (girl_i, girl_v) in enumerate(girls):
            if not girls_visited[girl_i] and is_prime(boys[boy_i] + girl_v):
                girls_visited[girl_i] = True
                if girls_matched[girl_i] is None or find_girl(girls_matched[girl_i]):
                    girls_matched[girl_i] = boy_i
                    return True
        return False

    girls_matched = [None] * len(girls)
    for (boy_i, boy_v) in enumerate(boys):
        girls_visited = [False] * len(girls)
        find_girl(boy_i)
        # print(girls_matched)
    ans = len([i for i in girls_matched if i is not None])
    print(ans)
    return ans


if __name__ == '__main__':
    s = '''58
    621 10618 19556 29534 25791 11133 5713 26642 25994 16095 6618 11447 29386 24436 22551 21467 2633 25704 29460 24325 8964 4087 10560 6478 9615 5119 1114 6773 9409 21549 15336 18995 2151 27404 6296 21066 3147 27037 6177 5650 16224 14352 8999 991 3012 16447 17799 16265 27163 24118 9766 15355 6161 3909 19451 16838 9113 10877'''
    main(s.splitlines()[1])

该题总结

很多题，如果解决问题的方法上偏了，就很难解决了。就像这道题，如果不知道匈牙利算法，不知道图论的一些知识，就很难做出来。

不过，这道题还有一个更大的杀器：带树开花算法。该算法可用于解决一般图的最大流问题，由于该题只是二分图的匹配，因此就没必要使用这么通用/底层/复杂的算法了。这个有时间再补吧！

华为 OJ 所有难题总结

总体来说，没有想象中那么难，按照我的这三篇文章来刷，三天时间（或者一天）即可全部掌握。

Anyway，暴力搜索、DFS、BFS、回溯、动态规划、数论、图论（例如最短路径），这些个概念还是比较重要的，在此基础上再好好研究一下对字符串的操作（比如正则匹配的基本实现）与位运算，可以拿下绝大多数算法题。

我们下期再见！