王曼妮的择偶问题（二分流匈牙利算法）

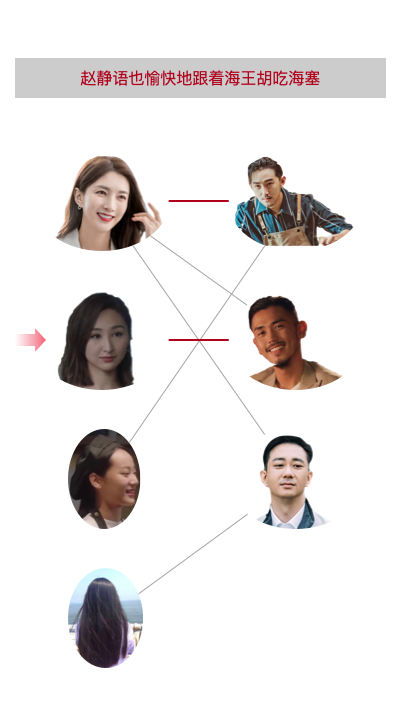
王曼妮红线模型之原理——匈牙利算法

在上述模型中，将所有对象分成男方和女方两组，这就是所谓的二分图。

每个子图里有多个对象，即节点。每个节点只与另一个子图里的节点连接，可以为 0 到多个。

我们模型的优化目标，就是为尽可能多的节点连线。而约束条件就是：每个节点具有唯一占有性质，即当该节点与某一个节点连接后，其他节点不得再与该节点连接。（像极了爱情里的坟墓）

解决这个模型的方法有很多种，而大名鼎鼎的匈牙利算法就是解决该问题的最优秀方法之一，易于理解，效果拔群。

匈牙利算法是一种在多项式时间内求解任务分配问题的组合优化算法，并推动了后来的原始对偶方法。美国数学家哈罗德·库恩于 1955 年提出该算法。此算法之所以被称作匈牙利算法，是因为算法很大一部分是基于以前匈牙利数学家 Dénes Kőnig 和 Jenő Egerváry 的工作之上创建起来的。（来自百度百科）

对该算法的英文讲解，可以参考：http://www.hungarianalgorithm.com/examplehungarianalgorithm.php

该算法的多目标追踪应用，可以参考：https://zhuanlan.zhihu.com/p/62981901

匈牙利算法的编程实现

"""
使用一个二维矩阵记录节点对应关系
1表示匹配，0表示不匹配
每一行表示一个女孩的倾向
同理，每一列是一个女孩对男孩的倾向
"""
arr = [
    [1, 1, 1],
    [0, 1, 0],
    [1, 0, 0],
    [0, 0, 1]
]

# 使用一个一维数组记录右边子图的匹配状态
boys_matched = [None] * len(arr[0])

"""
对于每一个女孩，遍历寻找是否有能匹配成功的男孩
在遍历时，若对该男孩本身无兴趣，则跳过（矩阵中对应位置为0）
若有兴趣，且该男孩未有主，则直接匹配，并标记占有
若有兴趣，但该男孩已经有主，且已访问过，则跳过
若有兴趣，但该男孩已经有主，且未访问过，则尝试对系统进行回溯
若遍历结束也未能寻找到能匹配的男孩，则不对该女孩进行匹配
"""
def find_boy(girl_i):
    # 遍历第i个男孩的女孩列表，如果能成功找到一个让所有人满意的女孩，则为该男孩与该女孩进行标记
    for (boy_i, boy_like) in enumerate(arr[girl_i]):
        if boy_like and not boys_used[boy_i]:
            boys_used[boy_i] = True
            # 如果女孩未被抢走，或者通过回溯能够让所有人满意，则进行标记
            if boys_matched[boy_i] is None or find_boy(boys_matched[boy_i]):
                boys_matched[boy_i] = girl_i
                return True
    return False

这个算法的关键在于，不但要有一个boys_matched全局一维数组记录每个男孩的匹配情况，还要有一个boys_visited局部数组记录每个男孩的访问情况，这个数组在遍历每个女生时重置。

因此，主循环写成如下。

if __name__ == '__main__':

    # 主循环，对二分图的左边，即矩阵的行进行遍历
    for (girl_i, girl_preference) in enumerate(arr):
        # 重置访问数组
        boys_used = [False] * len(girl_preference)
        find_boy(girl_i)

    # 输出最终结果
    for (i, j) in enumerate(boys_matched):
        print(f'{i} -- {j}')

结果如下。

0 -- 2
1 -- 1
2 -- 0

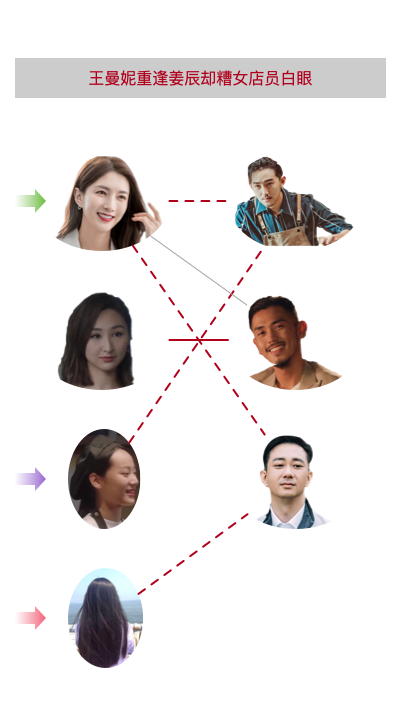
也就是 0 号女生（王曼妮）与 2 号男生（张志）匹配，1 号女生（赵静语）与 1 号男生（海王）匹配，2 号女生（咖啡店店员）与 0 号男生（咖啡店店主）匹配。

完全符合我们图里的描述与思路。

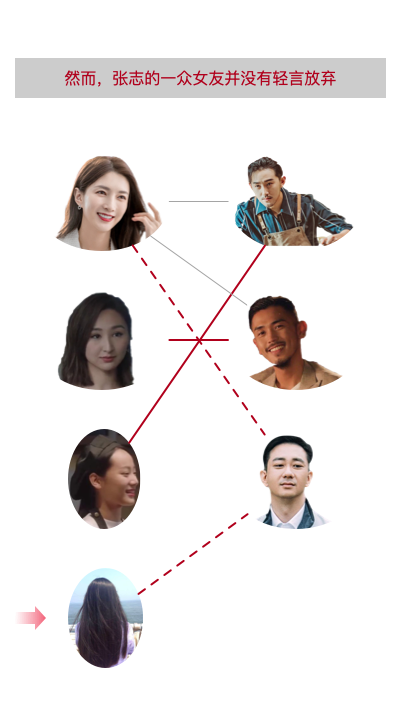
然而。。。

爱情里最真实的样子

结语

前段时间两天看完《三十而已》，还是很有感触的。

这首先是因为三十对于自己来说，也是一个即将到来的日程。其次取材地点在上海，也是我近年来经常工作的城市。此外，还有浓浓的金融风（尽管多是讽刺寓意），这些都与我息息相关。

近期恰好在研究算法时遇到匈牙利算法，觉得很适合用它去描述与理解一些问题。

不过，在肯定该算法的同时，也必须指出，该算法只是一个双向连线模型，没有考虑线的权重。如果我们在该模型的基础之上考虑线的权重，其实可以更加吻合编剧对该剧的发展期望的。比如我们设王曼妮对姜辰、海王、张志的权重为 0.1、0.4、0.2，对其他人的权重为 0.3；等等。

算法归算法，只是一种思想。而模型归模型，其本身尚不具备完全解释现实的能力。人在世界上，很多决策都是基于复杂环境的应变反应，具有较大不确定性，况且还有类似王曼妮最后甩手十万就去欧洲留学的迷之决策……

希望本篇文章对你的某些方面有所启发。

下期再见！

作者：南川

制图：南川

编程：南川