
挣 1000 万,真地比中 1000 万难太多了吗?
如果按照某团骑手的目标工资 1w/month 的水平来看的话,不考虑通胀、不考虑意外、不考虑衰老、不买房至多可以在 1000/12≈83 年内可以实现。
这已经大大超过为祖国健康奋斗五十年的期限,看样子是不太可能实现的目标。
那买彩票可以吗?比如中国体育彩票。我们今天就来我们算一算。
大乐透模型搭建与分析
大乐透的中奖概率分析
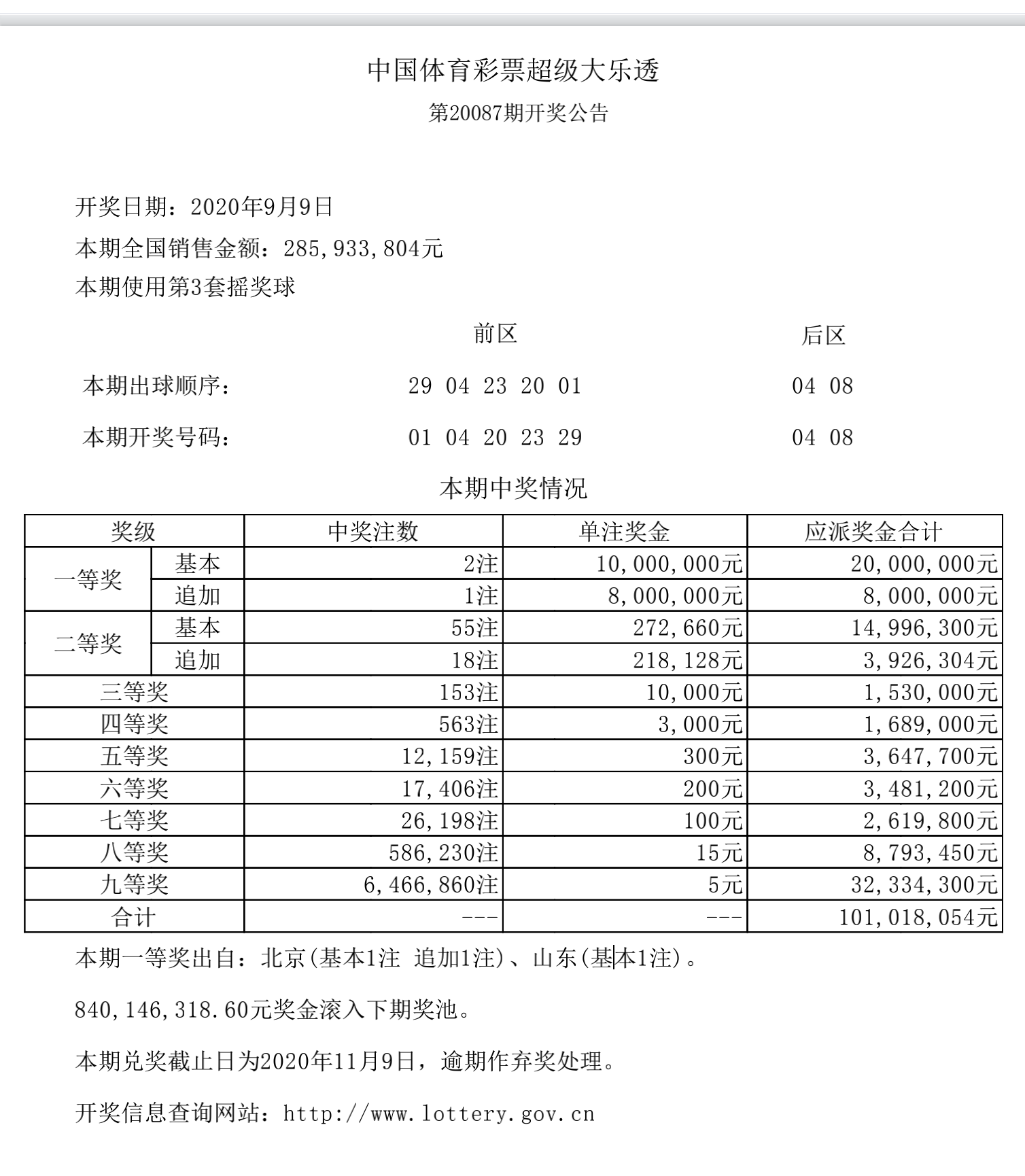
以中国足彩官网超级大乐透的第一大奖为例,可以看到,单注奖金高达一千万,根据规则一注 1 元。目前总销售额接近 3 亿元,滚动奖金总共 8 亿元。因此,我们可以简单假定中奖概率为一亿分之一,也就是1e-8,而赔率为一千万。
大乐透的投资模型搭建
我们首先搭建一个投资回报模型。
记每一笔赌注需要花费 1 元,一笔赌注的胜率为$p$,则失败的概率为$1-p$,赌赢的收益率为$q$,赌输的收益率为$r$。因此,对于大乐透头奖来说,有以下模型变量:$p=1e-8,\ q=1e7,\ r=-1$。
此外,我们记自己的本金为$a_0$,其中用于购买彩票的比率为$k, \ (a_0*k < 1 / p)$。显然,在不考虑注上限、游戏是公平的情况下,我们每一次决策的结果有两种可能。
- 若中奖,我们的本金变成 $a_0*(1-k)+q$。
- 若没有中奖,我们的本金变成 $a_0*(1-k)$。
考虑到目前的人均收入水平,我们简单假设每个人的本金是 10w,则该模型可简化为:
- 若中奖,我们的本金变成 $10*(1-k)+1000$。
- 若没有中奖,我们的本金变成 $10*(1-k)$。
显然,在这个模型里,若 k 不等于 0,则最小为$1e-5$,也就是十万分之一。
我们每个人都要思考几个问题:
- 你会购买至少一注大乐透吗?用大概率会浪费的 N 元,去博取 1000w?
- 你会长时间的购买 N 注大乐透吗?为什么?
大乐透的投资模型分析(一):按比率投资模型
我们首先考虑按比率投资模型,也就是说,张三本金$a_0=10$万,工作收入与支出完全平衡,每天按照一定比率$k$购买大乐透彩票,持之以恒,夜以继日。求其能中一千万的概率。
那么,对于第一次能中的概率,即为$a_0pk$,其中$a_0$是本金,$p$是每一注中奖的概率,大乐透头奖概率为$1e-8$,$k$为支付比率,$10k$得到最终的以元为单位的价值,不考虑小数。我们可以很容易列出每一次投资时的状态。

| 投资次数 | 投资前本金 | 累计获胜概率 |
|---|---|---|
| 1 | $a_0$ | $a_0kp$ |
| 2 | $a_0*(1-k)$ | $a_0kp + a_0(1-k)kp$ $=a_0kp[1+(1-k)]$ |
| 3 | $a_0*(1-k)^2$ | $a_0kp*[1+(1-k)+(1-k)^2]$ |
| i | $a_0*(1-k)^{i-1}$ | $a_0kp*\frac{1-(1-k)^i}{k}$ |
当然了,由于$\lim\limits_{i\to+\infty}{a_0kp\frac{1-(1-k)^i}{k}}=a_op$,所以若无限投资下去,概率就等于本金乘以每一注中奖的概率,emmm,所以若想自己中奖的期望概率能够达到百分之百,得首先有……有一千万。
于是,能不能通过中奖得到一千万,从概率上几乎等价于能不能通过自己挣到一千万。。。。
惊不惊喜,意不意外?
大乐透的投资模型分析(二):按固定投资模型
我们接着考虑按固定投资模型,也就是说,张三本金$a_0=10$万,工作收入与支出完全平衡,每天按照固定的金额购买大乐透彩票,持之以恒,夜以继日。求其能中一千万的概率。
考虑到,按照大多数人的风险偏好,一般只会顺手买一注,毕竟买一注和买两注本质上没啥差别,但今天一下亏两注绝对不如每天只亏一注心理负担来的小。但便于方程求解,我们还是设置一个固定常量,记为$c$,表示每天的购买支出,于是每天中奖的概率都是$c*p$,雷打不动。
显然,这就是一个典型的伯努利试验,我们知道它的期望成功概率就等于$ncp$,让其等于 1,则立即得到$n*c=\frac{1}{p}$,即所有付出的投资总和需要与最终奖金相同。。。
于是,能不能通过中奖得到一千万,从概率上几乎还是等价于能不能通过自己挣到一千万。。。。
惊不还惊喜,意不还意外?
大乐透投资模型(白努力模型)总结
其实无论是采用按比率投资的方式,还是按固定投资的方式,之所以最后我们算出来期望中奖概率为 1 时所需要的资金正好等于奖金额度,其本质就在于因为它每一次都是一个平等的伯努利实验,只不过我们按天划分,做了一些伪装而已。
如果你觉得我们的模型结论让你觉得意料之中又情理之中,那恭喜你,成功地被我们绕进去了。
但为了更好地回答大乐透,以及由此衍生的一切赌注模型,我们先从另一个案例说起。
另一种看起来简单点的赌注模型
假设你有 100 万,面临一个赌注,50%概率能赢,获得三倍,50%会输,你会如何抉择?
先给你十秒钟思考。
基于风险偏好的不确定性投资
我猜大多数人都会基于自己的风险偏好去决定这笔赌注。
具体来说,假如我们把一个人的资金分成几个部分:生活必需资金(10 万)、发展必需资金(80 万)、可投资资金(10 万)。
那么面临这样的一个赌注,如果这个人风险偏好非常高,他可能就会把全部 10 万都投进入;反之,则可能不会参与如此高风险的赌注。
每个人心里都有自己的一种考虑,因此这道题是无解的。
但学过概率论与一定经济学原理的我们,不妨换个角度想想,我们每次要做一个决定时,依据究竟是什么。
诚然,大多数生活中的决策,都是依据于目标收益和短期融资需求,在大多数情况下,一旦某个赌注目标收益很高,而自己的短期融资需求也同样很高,那么他选择铤而走险的概率就很大了。由于生活中不存在明确的投资产生回报的概率,这是最典型一种决策依据。
但如果我们知道概率呢?就如同之前的彩票问题一样。那么借助于概率统计的角度去思考,应该是第一思考方式了。
我们据此想想,这样的模型,基于概率统计,我们能够有哪些种决策依据,换句话说,我们的投资目标是什么。
基于目标收益的确定性投资
如果我们的投资目标就是为了获得收益,无视风险,那就把所有的钱都砸进去好了。反之,如果我们的目标就是为了规避风险,那么我们应该坚决不参与本次赌注。还有另外一种,比较现实的投资目标:跑赢通胀。简单来说,他的目标收益就是 10%,那么我们来算一下,如果是这样的一个目标,他应该投多少。
显然,如果一个人的投资目标是 10%,他应该想表达的是,他的期望收益是 10%,于是我们很容易得到以下的方程:
$0.5 (100-x+3x) + 0.5(100-x) = 100 * (1+0.1)$
答案很简单,$x=20$,即若该投资者从 100 万中取出 20 万参与该赌注,则能获得 10%(即 10 万)的目标收益。
在大多数情况下,基于一个固定的目标收益,去决定一项投资是否参与,属于比较靠谱的一种投资思维。
但也许并不够好。
假设该笔赌注是固定的,你可以参与无限多次,这个时候你再审视一下自己基于目标收益的投资理念是否靠谱?答:靠谱。因为每次就盯着 10%的目标收益不变,无论执行多少次,这个策略是完全 make sense 的。
基于此,我们使用程序的手段,看看,如果我们把该赌注重复执行 N 次看看最终我们能赚多少钱。
首先,显然,我们很容易得到,如果我们的目标收益固定,例如$E=10$,则必有每次投入的资金比率为$K=2*E=20\%$。
因此,我们可以使用程序模拟如下的场景:固定的本金(100 万),11 个人,每次投入的本金比率不同(从 0%到 100%,步长为 10%),每个人连续赌十次,看看最终大家的收益水平如何。(显然,0%的哥们最终依旧是 100 万不变)
我们编写程序模拟该过程。
import random
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.sans-serif'] = ['SimHei', 'STHeiti'] #显示中文标签
plt.rcParams['axes.unicode_minus'] = False
A = 100 # 本金(单位:万)
P = 0.5 # 中奖概率
R = 3 # 中奖赔率
T = 11 # 参与者个数
LU = 1 # 10的指数上限
LD = 0 # 10的指数下限
N = 10 # 赌注次数
def simulate_by_ratio(k):
cur_asset = A
assets = [cur_asset]
for day in range(N):
pay = cur_asset * k
cur_asset -= pay
if random.random() < P:
cur_asset += pay * R
assets.append(cur_asset)
return assets
arr = [simulate_by_ratio(k) for k in np.linspace(LD, LU, T)]
data = pd.DataFrame(arr).T
data.columns = ['{: 3d}%'.format(int(100*k)) for k in np.linspace(LD, LU, T)]
title = f'本金:{A}, 中奖概率: {P}, 中奖赔率: {R}, 赌注次数: {N}, 参与者:{T}'
ax = sns.relplot(data=data, kind='line', dashes=False).set(title=title)
ax._legend.set_title('投资比率')
plt.show()
得到结果如下。
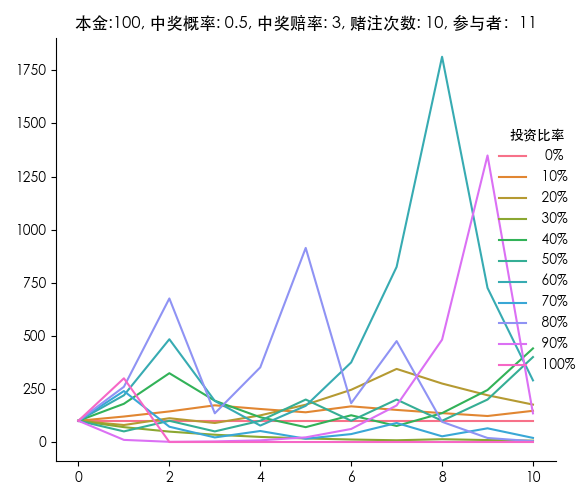
可以看到,整体来说,大多数人的收益波动都比较明显,整体还是呈现较好的预期,毕竟这个赌注的期望收益是正的。
但我们依旧难以确定一个最佳的投资目标。因此,新的维度需要引入。
基于长期最大期望收益的确定性投资
其实当我们设定了一个目标收益之后,我们不但可以使用程序随机模拟出重复执行该策略 N 次的结果,我们还可以算出他们的期望。如果我们基于目标收益的最大长期期望进行赌注,那从统计角度来说,我们的策略就更加地稳健。
易知,对于第$i$次以$k$比率的赌注,我们的预期收益将是$E = [0.5 A(1-k+3k) + 0.5 A(1-k)] / A = 1 + k /2$.
但如果以这样的方式顺推计算,我们将会得到长期预期收益将为$E^N=(1+k/2)^N$,这是这个指数函数,显然不具有实际意义。
重新考虑。对于每一次赌注,我们可能赢,也可能输,而在 N 次赌注后,我们最终的收益水平将是$\bar{E} = A(1+2k)^S(1-k)^F$,其中$S$表示成功的次数,$F$表示失败的次数。那么显然,这个函数就有点像经济学中类似道格拉斯函数的存在了。
我们稍微整理一下,略去常量$A$,替换$S=Np, F=N(1-p)$,则有$f(k)=(1+2k)^{N/2}(1-k)^{N/2}$,接着对其对数求导,则有$ln(f(k))=N/2ln(1+2k)(1-k)$,显然,当$(1+2k)(1-k)$最大时$f(k)$最大,立即得$k=[-1/2+1]/2=1/4$。
所以,按照长期最大期望收益的目标,我们每一次的投资比率是 25%。
为了验证这一投资比率的有效性,我们再次使用蒙特卡洛模拟,运行十次,查看其运行的整体情况。
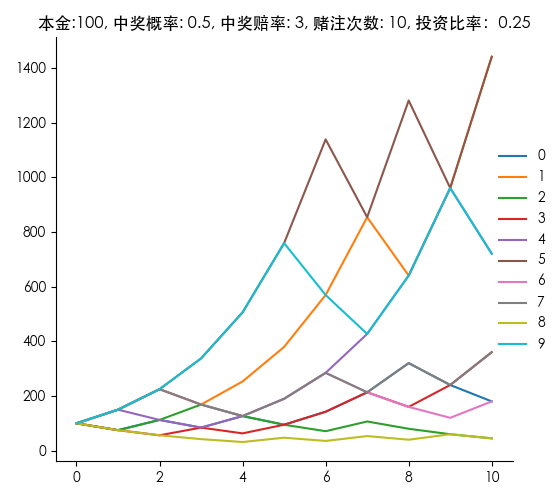
可以看到,整体效果还是很不错的,只有极个别案例出现了低于 100 的净值,大多数都有非常不错的表现,超过五倍收益的达到了 40%,这是相当耀眼的成绩。
一定程度上,这个长期最大收益的目标,的确很好地平衡了收益与风险,基于此,我们推广出其通用公式。
假设一项赌注,赢率为$p$,则输率为$1-p$。假设赢后收益率为$q$,输后收益率为$r$,本金为$A$,每一次固定下注比率$k$,重复$N$次,则有
对于第$i$次赌注,若赢,本金变为$ A_i(1-k)+A_ik(1+q)=A_i(1+kq)$;同样地,
对于第$i$次赌注,若输,本金变为$ A_i(1-k)+A_ik(1+r)=A_i(1+kr)$。
显然,对于累积 N 次赌注,必有$A_N = A_0 (1+kq)^S (1+kr)^F$,代入$S = N p, F = N (1-p)$,则有
$A_N = A_0 (1+kq)^{Np} (1+kr)^{N(1-p)}$,对数后得
$ln(A_N) = ln(A_0) + N (pln(1+kq)+(1-p)*ln(1+kr))$,即求
$max\ f(k) = p ln(1+kq) + (1-p) ln(1+kr)$,对其求导,则有
$max f'(k) = \frac{pq}{1+kq} + \frac{(1-p)r}{1+kr}$,显然直接令其等于 0 即可得到函数拐点,即
$(*)\frac{pq}{1+kq} + \frac{(1-p)r}{1+kr}=0$,则有
$()k=\frac{pq+(1-p)r}{-qr}$,其中分子就等于胜率乘以胜赔率加上输率乘以输赔率,分母则为负的胜率乘以赔率**。
而当$r=-1$时,则有,
$(***)k=\frac{p(q+1)-1}{q}$
我们验证一下,上一题中$p=1/2,\ q=2,\ r=-1$,(赌一赢三,收益率$q$为 2;全光,收益率为-1)
则有$k=\frac{1/22+1/2(-1)}{2}=\frac{1/2}{2}=\frac{1}{4}$,完全一致。
这,就是大名鼎鼎的凯利公式!
使用凯利公式重买大乐透
在概率论中,凯利公式(Kelly formula),也称凯利方程式,是一个用以使特定赌局中,拥有正期望值之重复行为长期增长率最大化的公式。
它由约翰·拉里·凯利(John Larry Kelly, Jr.)于 1956 年在《贝尔系统技术期刊》中发表,可用以计算出每次游戏中应投注的资金比例。(约翰·拉里·凯利 1923 年出生于美国德克萨斯州科西卡纳,1965 年逝世于纽约市,是一位在贝尔实验室工作的美国科学家)
当我们使用凯利公式时,我们清楚地明白,我们要做的事就是根据凯利公式,实现长期某项重复确定性概率投资的最终收益率最大化。而彩票明显符合这种特性。
回顾大乐透的一些基本变量,胜率$p=1e-8$,赔率$q=1e7$,那么显然有$k=\frac{p*(q+1)-1}{q}=\frac{(1e-8)(1e7+1)}{1e7}=1e-8$。
这意味着,如果你的身家没有一亿,那么哪怕赔率是一千万的大乐透,也不值得你花一块钱去购买它。
由此来看,比起中一千万,还是挣一千万来的更容易。
大喊一声:为祖国健康奋斗五十年,上路吧,兄弟姐们!上路吧,我的小蓝车和你的小黄车!
