关于正态分布表的一个有趣发现

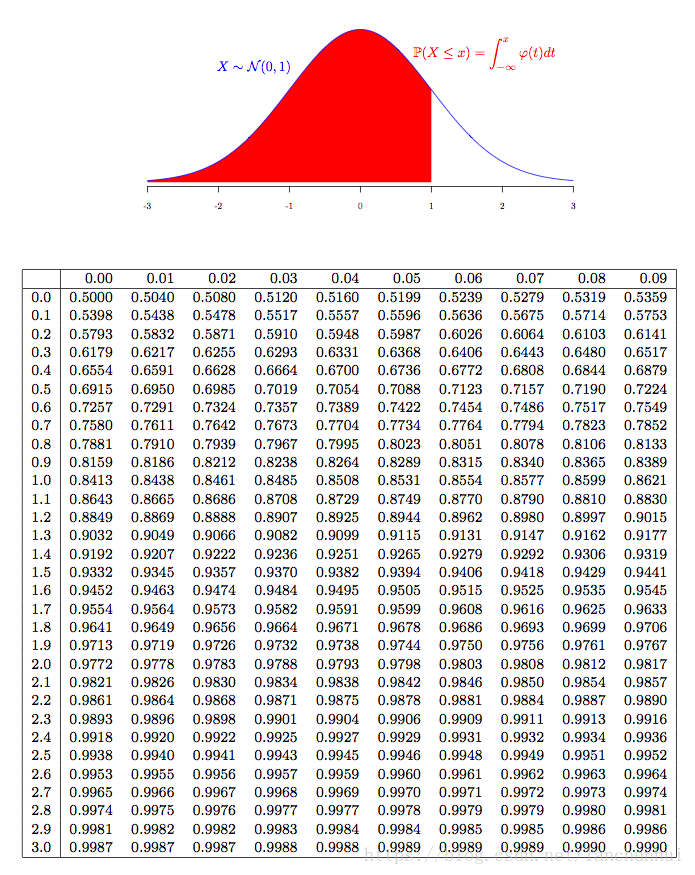
正态分布表

今天做到一道题，要用到 $\Phi (1)=0.84$和$\Phi(0.25)=0.6$，当然，这种数如果是考试肯定会直接给出相应的数值，具体等于多少不需要记。

但就在我去研究一下正态分布表后发现，几个特殊的值非常好记，也就是从$\Phi(0)=0.5$开始，你会发现，$x$每增加 0.25，$\Phi(x)$就增加 0.1，0.09，0.08，0.07（这个时候已经到$\Phi(1)$了），接着就跳过 0.06，增速变成 0.05,0.04,0.03,0.02,0.01,0。这也太有意思也太好记了！

很容易知道，比如说九坤这家公司的口号是招聘市场上两个$\sigma$之外的人才，我都不用记$\Phi(2)$是多少，

直接心酸算

$$ n = 2 \times 4 = 8\ di = 0.1, 0.09, ..., \ \sum{i=1}^{n} {di}=\dfrac{(0.10+0.02)*9}{2} - 0.06 = 0.48\ \therefore \Phi(2) =\Phi(0)+\sum{i=1}^{n}{d_i}= 0.5 + 0.48 = 0.98 $$

也就是 Top 2%。

x	$\Phi(x,2)$	$\Delta \Phi(x, 2)$
0	0.5
0.25	0.6	+0.1
0.5	0.69	+0.09
0.75	0.77	+0.08
1	0.84	+0.07
1.25	0.89	+0.05
1.5	0.93	+0.04
1.75	0.96	+0.03
2	0.98	+0.02
2.25	0.99	+0.01
2.5	0.99	+0
2.75	1
3	1

关于昨天那道题

题目

甲乙二人轮流投篮，甲先开始，甲每轮投一次，乙每轮投两次，甲乙每次投篮命中率分别为 p 和 0.5，求当 p 等于多少时，甲乙胜负概率相等

解答

$$ \begin{align}

\because \left{ \begin{array}{l} P(甲胜) & = p + (1-p)\times \frac{1}{4}\times P(甲胜) & = \dfrac{4p}{3+p} \

P(乙胜) & = (1-p)\times \frac{3}{4} + (1-p)\times \frac{1}{4}\times P(乙胜) & = \dfrac{3(1-p)}{3+p} \ \end{array} \right . \newline

\begin{array}{l} \therefore P(甲胜) = P(乙胜) & = > 4p = 3(1-p) & = > p = \frac{3}{7} &&&&&& \end{array}

\end{align} $$

评注

这题来自全书，答案是用模拟每次投篮做的，写的很繁，但是用我们昨天讨论的不变式去做就非常简单与快速。

不过要小心，这种解法只适合“无记忆性”的题目，即新的每一轮几乎与过去没啥关系，假如我们加个约束条件，比如假定 10 轮内甲乙胜负概率相等，那就只能用模拟法了，因为已经发生的 k 轮对接下来的 10-k 轮的讨论可能有影响。

关于无记忆性的指数分布

指数分布是无记忆性的，即当$x>0$时，$P(X>s+t | X>s)=P(X>t)$，它常用来描述一些电子元器件的使用寿命。

这不禁让我豁然开朗，怪不得众多手机都不给出电池的预期使用寿命，毕竟服从指数分布，意味着假如期望寿命是一年的话，一年后电池如果没话，说明还能继续再用一年……以此类推……

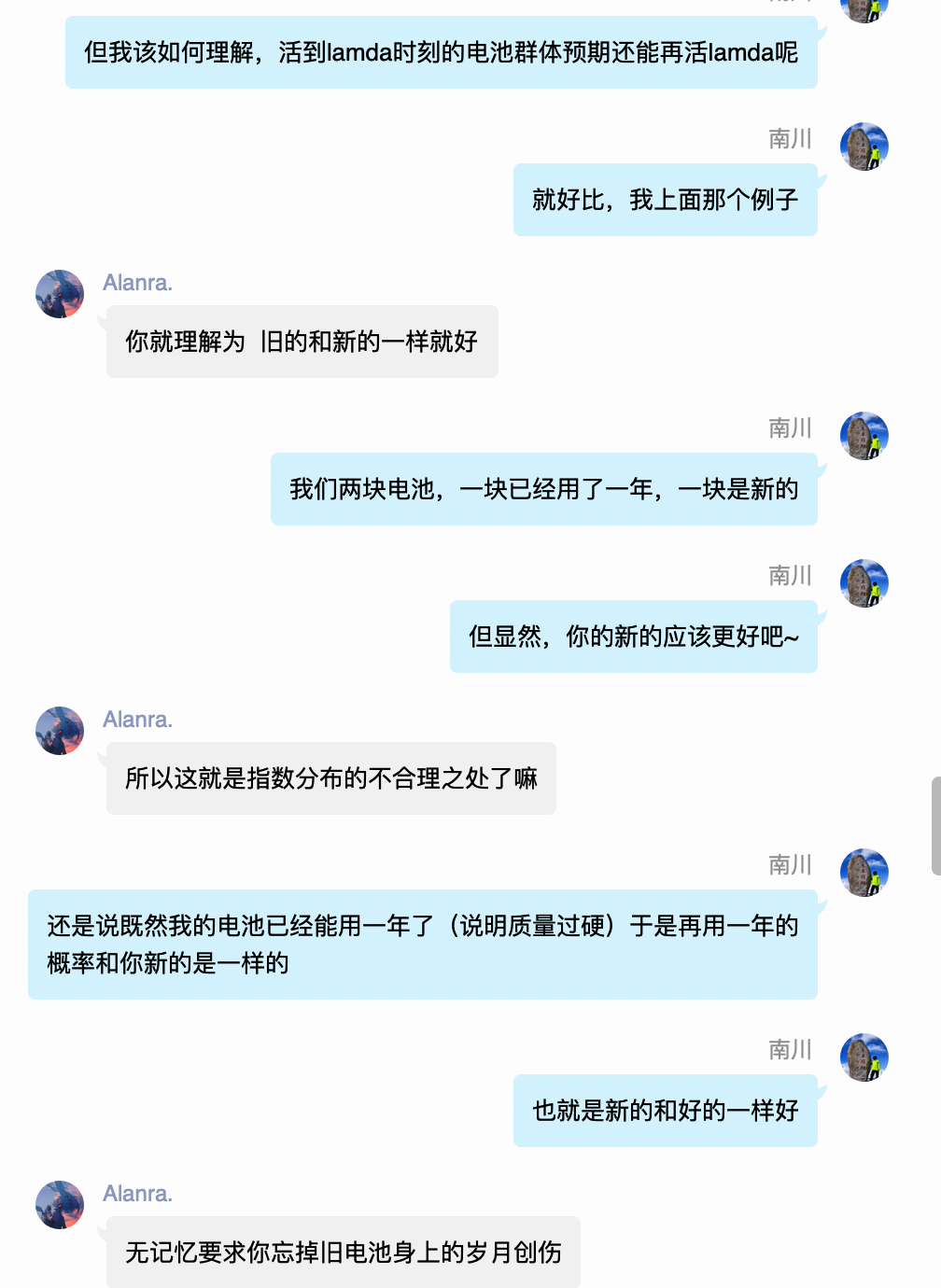
基于这个结论，我突然想起一部剧：

国立：
哥啊，这人生的路怎么那么难走啊！
葛优：
可不是！
打在胎里就随时有可能流产当妈的一口烟就可能长成畸形长慢了心脏缺陷长快了就六指好容易扛过十个月生出来了一不留神还得让产夹钳把脑袋夹扁了都多过去了小儿麻痹百日咳猩红热大脑炎还在前边等着呢哭起来呛奶走起来摔跤摸水水烫碰火火燎是个东西撞上咱就是个半死钙多了不长个钙少了吧罗圈腿总算混到会吃饭能出门了天上下雹子地下跑骑车大街小巷是个暗处就躲着坏人你说赶上谁都是个九死一生不送命也得落个残疾
国立：
这都是明枪还有暗箭呢势利眼冷脸子闲言碎语指桑骂槐好了遭人嫉妒差了让人瞧不起忠厚人家说你傻精明了人家说你奸冷淡了大伙说你傲热情了群众说你浪走到前边挨闷棍走到后边全没份

听起来很有道理，但我们似乎过于感性了，再仔细想想，会发现人的寿命或者生存能力啊，就有点像这指数分布，你一定熬过去了，在新的起点，能再活多少年的期望，和新人是一样（而非衰减）的！

所以人生路虽难，人却并不脆弱，反而更有可能越挫越勇，最终泰山崩于前而色不变，无惧生命中任何波澜。

网友注脚：“但是生而为人，我很精彩！就凭这九死一生我也得打起精神去走一走那非线性人生！”大抵也是这个意思吧~